機器學習之樸素貝葉斯算法(上)
1.算法概述
在機器學習中����,有許多算法����,大致可以分成分類算法和回歸算法��,分類算法有K近鄰�����、樸素貝葉斯�、決策樹����、隨機森林�����、邏輯回歸�、神經網絡等等�����,回歸算法有線性回歸����、嶺回歸等等��。樸素貝葉斯算法作為分類算法之一���,它簡單高效���,在處理分類問題上�����,是應該首先考慮的方法之一��。
本篇文章主要是介紹樸素貝葉斯算法涉及到的數學知識概率論相關知識
2.隨機試驗
滿足以下三個特點的試驗稱為隨機試驗:
–可以在相同的條件下重復進行�。
–每次試驗的可能結果不止一個�����,并且能事先明確試驗的所有可能結果�����。
–進行一次試驗之前不能確定哪一個結果會出現�。
舉例:
–E1:拋兩枚硬幣���,出現正面H�、反面T的情況����。
–E2:拋一枚骰子����,觀察可能出現的點數情況�。
3.樣本點����、樣本空間�����、隨機事件
樣本點(sample point):隨機試驗的每一個可能的結果稱為樣本點��,用e表示�。
樣本空間(sample space):隨機試驗E的所有可能結果組成的集合�����,記作S�����,即S={e1�,e2�����,…��,en }.
隨機事件(random variables events ):樣本空間S的任一子集A��。屬于事件A的樣本點出現�����,則稱事件A發生�����。特別的����,僅含一個樣本點的隨機事件����,稱為基本事件���。
舉例:
隨機試驗:拋一枚骰子���,觀察可能出現的點數情況�����。
樣本空間為:S={1���,2��,3���,4�,5��,6}
樣本點為:ei=1���,2���,3��,4����,5��,6.
隨機事件A1:“骰子出現的點數為5”����,即A1={x│x=5}
4.隨機變量
隨機變量(random variable): 表示隨機試驗各種結果的實值單值函數��。
舉例1:隨機試驗:拋兩枚骰子����,觀察可能出現的點數的和�����。試驗的樣本空間是S={e}={(i��,j)|i�,j=1��,2���,3�,4�����,5���,6}�����,i��,j分別是第1次�,第2次出現的點數�,以X記為兩球號碼之和�����,則X是一個隨機變量�����。
X=X(e)=X(i����,j)=i+j�,i���,j=1��,2�����,?�,6.
?舉例2:隨機試驗E1:拋兩枚硬幣��,出現正面??����、反面??的情況�。試驗的樣本空間是S={HH���,HT�����,TH���,TT}�,以Y記為兩次投擲硬幣得到反面T的總數�����,則Y是一個隨機變量���。
5.概率與條件概率
貝葉斯算法是基于條件概率的一種算法����,接下來我們先理解一下概率及條件概率的概念��。
概率亦稱“或然率”�。它反映隨機事件出現的可能性(likelihood)大小��。隨機事件是指在相同條件下�,可能出現也可能不出現的事件����。例如����,從一批有正品和次品的商品中���,隨意抽取一件����,“抽得的是正品”就是一個隨機事件�。設對某一隨機現象進行了n次試驗與觀察���,其中A事件出現了m次�,即其出現的頻率為m/n����。經過大量反復試驗�,常有m/n越來越接近于某個確定的常數(此論斷證明詳見伯努利大數定律)����。該常數即為事件A出現的概率����,常用P (A) 表示�����。
條件概率�����,是指事件A在另外一個事件B已經發生條件下的發生概率
在很多情況下�,我們感興趣的是某個事件在給定其他事件發生時出現的概率����,這種概率叫做條件概率:
P(Y│X)=(P(YX))/(P(X))
聯合概率���, 是指在多元的概率分布中多個隨機變量分別滿足各自條件的概率�����。假設X和Y都服從正態分布�����,那么P{X<4,Y<0}就是一個聯合概率��,表示X<4,Y<0兩個條件同時成立的概率�����。表示兩個事件共同發生的概率�。A與B的聯合概率表示為 P(AB) 或者P(A,B),或者P(A∩B)
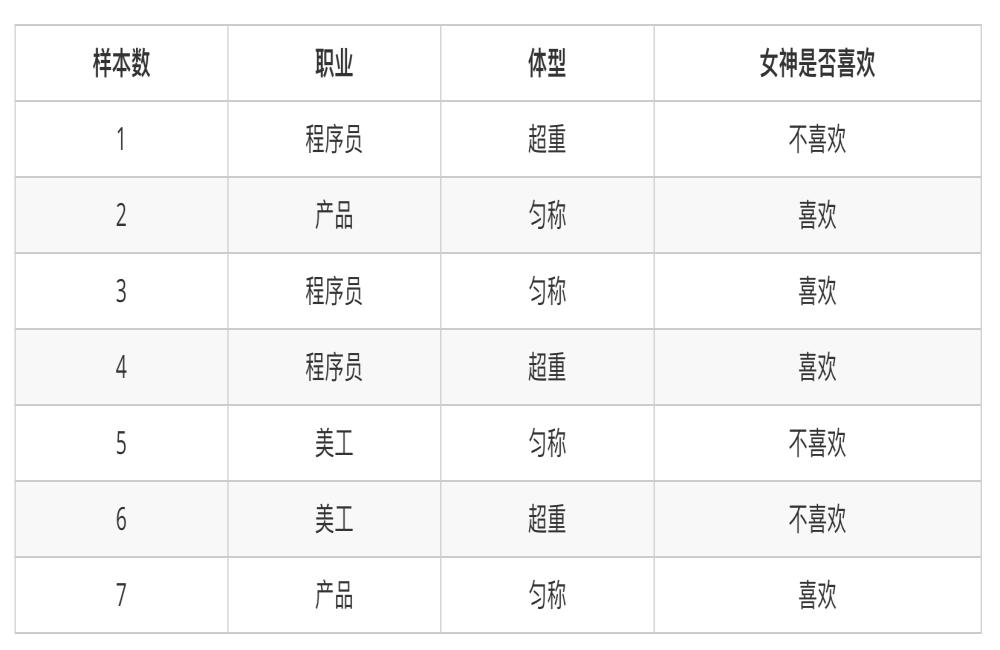
例如有以下樣本數據
 ?
?
問題:
1�����、女神喜歡的概率����?
2��、職業是程序員并且體型勻稱的概率�����?
3�����、在女神喜歡的條件下���,職業是程序員的概率�?
4�、在女神喜歡的條件下��,職業是產品��,體重是超重的概率�����?
分析以上樣本數據����,得出來的答案如下:
1��、女神喜歡的概率�?
此題屬于概率問題�,女神喜歡的有4個樣本數據���,不喜歡的有3個樣本數據����,所以女神喜歡的概率是 4/7
2��、職業是程序員并且體型勻稱的概率���?
此題屬于聯合概率問題�����,職業是程序員的概率是3/7���,體型勻稱是4/7�����,因此�,職業是程序員并且體型勻稱的概率是3/7*4/7=12/49
3��、在女神喜歡的條件下�����,職業是程序員的概率����?
此題屬于條件概率問題��,女神喜歡的有4個數據樣本���,在女神喜歡的條件下�,職業是程序員的概率2/4
4����、此題屬于聯合概率問題�,按聯合概率對此問題可以進行分解
P(女神喜歡|(職業是產品,體重是超重))=P(女神喜歡|職業是產品∩女神喜歡|職業是程序員)=1/4*1/2=1/8
此篇文章主要是介紹樸素貝葉斯算法的概率基礎��,下一篇文章將會介紹樸素貝葉斯算法原理及相關案例����。


 ?
?